Voxel time courses¶
When we have a 4D image, we can think of the data in several ways. For example the data could be:
- A series of 3D volumes (slicing over the last axis);
- A collection of 1D voxel time courses (slicing over the first three axes).
>>> # Load 4D image file
>>> import nibabel as nib
>>> img = nib.load('ds114_sub009_t2r1.nii')
>>> img.shape
(64, 64, 30, 173)
We drop the first volume; as you remember, the first volume is very different from the rest of the volumes in the series:
>>> # Drop the first volume
>>> data = img.get_data()
>>> data = data[..., 1:]
>>> data.shape
(64, 64, 30, 172)
We can think of this 4D data as a series of 3D volumes. That is the way we have been thinking of the 4D data so far:
>>> # This is slicing over the last (time) axis
>>> vol0 = data[..., 0]
>>> vol0.shape
(64, 64, 30)
We can also index over the first three axes. The first three axes in this array represent space.
- The first axis goes from right to left (0 index value means right, 63 means left);
- The second axis goes from back to front (0 index value means back, 63 means front);
- The third axes goes from bottom to top (0 means bottom, 29 means top).
If you give me index values for these first three axes, you have given me a coordinate in the first three axes of the array.
For example, you could give me an index tuple for the first three axes like
this: (42, 32, 19). The first index of 42 refers to a position towards the
left of the brain (> 31). The second index of 32 refers to a position almost
in the center front to back. The last index of 19 refers to a position
a little further towards the top of the brain — in this image.
This coordinate therefore refers to a particular part of the image:
>>> # Where is this in the brain?
>>> mean_data = np.mean(data, axis=-1)
>>> # Make a nice bright dot in the right place
>>> mean_data[42, 32, 19] = np.max(mean_data)
>>> plt.imshow(mean_data[:, :, 19], cmap='gray', interpolation='nearest')
<...>

If I slice into the data array with these coordinates, I will get a vector, with the image value at that position (43, 32, 19), for every point in time:
>>> # This is slicing over all three of the space axes
>>> voxel_time_course = data[42, 32, 19]
>>> plt.plot(voxel_time_course)
[...]
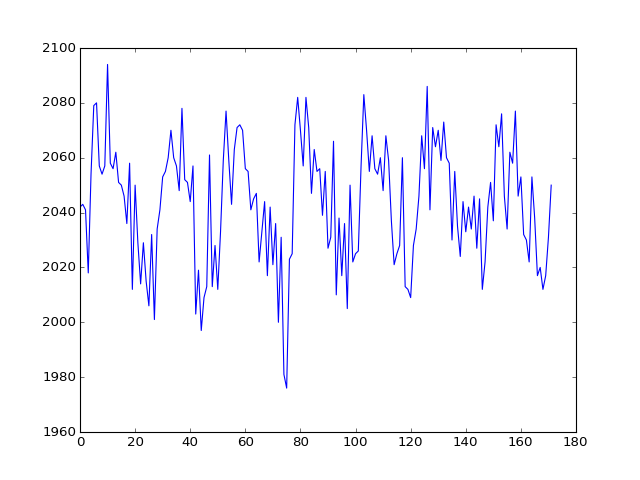
We could call this a “voxel time course”.
We might want to do ordinary statistical type things with this time course. For example, we might want to correlate this time course with a measure of whether the subject was doing the task or not.
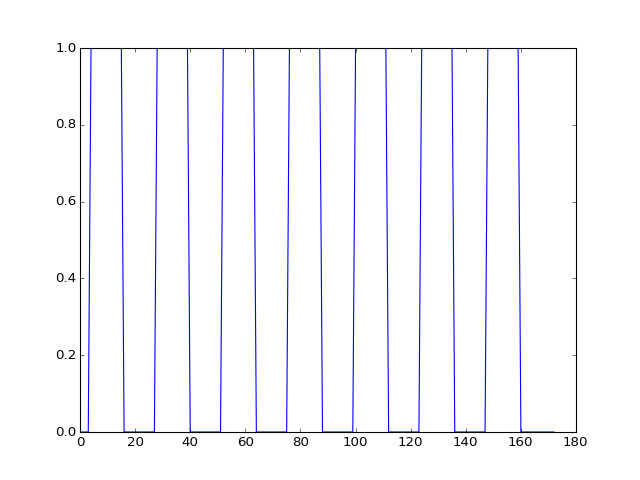
This measure will have 1 for each volume (time point) where the subject was doing the task, and 0 for each volume where the subject was at rest.
We call this a “neural” time course, because we believe that the nerves in the relevant brain area will switch on when the task starts (value = 1) and then switch off when the task stops (value = 0).
To get this on-off measure, we will use our pre-packaged function for OpenFMRI data:
>>> # Load the neural time course using pre-packaged function
>>> from stimuli import events2neural
>>> TR = 2.5 # time between volumes
>>> n_trs = img.shape[-1] # The original number of TRs
>>> neural = events2neural('ds114_sub009_t2r1_cond.txt', TR, n_trs)
>>> plt.plot(neural)
[...]
We can plot the voxel time course against this neural prediction:
>>> # Plot the neural prediction against the data
>>> neural = neural[1:]
>>> # Notice the + to specify the "line marker"
>>> plt.plot(neural, voxel_time_course, 'o')
[...]
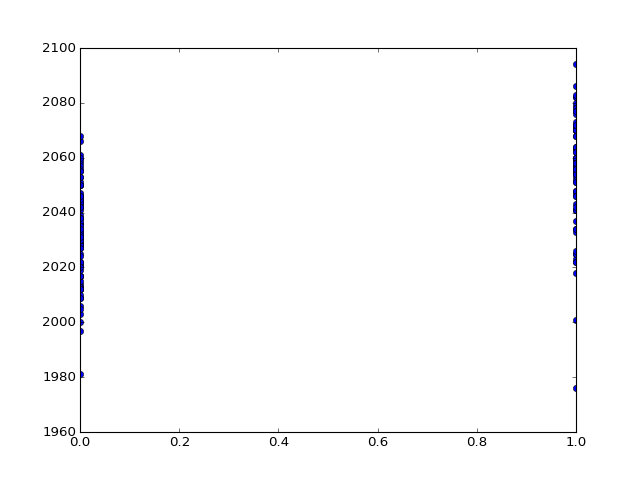
We can do things like get the correlation between the on-off prediction and the voxel time course:
>>> # Correlate the neural time course with the voxel time course
>>> np.corrcoef(neural, voxel_time_course)
array([[ 1. , 0.54285],
[ 0.54285, 1. ]])
