Text Mining¶
Contents
The process of deriving “meaningful” or “useful” information from text is called text mining. This includes information retrieval, lexical analysis (e.g., identifying the individual units of meaning in a text), statistical summaries, pattern analysis, and visualization techniques.
This is a very brief introduction to the field and will focus on a few specific topics. Specifically, I will discuss information retrieval from websites, a variety of data serialization methods, representing text as a bag of words in a term-document matrix, and dimension reduction using principle component analysis.
Websites¶
Many data sources are available on the Internet. You’ve probably used a web browser interface to search through some of this data and even download it to your computer. As you may have noticed, this manual process is labor intensive, error prone, and hard to document.
The two most common ways to automate information retrieval from websites are webscraping and working with webservices.
Webscraping¶
Webscraping is process of getting “unstructured” data on the World Wide Web into a structured format that allows you to store and analyze it. There are a number of methods for doing this. The easiest to understand and most labor intensive method is to manually copy-and-paste the information. A bit more automated technique is to use text grepping.
Another technique is to use an HTML parser. For instance, Thomas Kluyver’s webscraping example IPython notebook is a good place to start.
To get an interactive version of it, you can do the following from your BASH prompt:
$ git clone https://github.com/dlab-berkeley/python-fundamentals.git
$ cd python-fundamentals/cheat-sheets/
$ ipython notebook Web-Scraping.ipynb
Webservices¶
To provide programmatic and automatic interaction with their data stores, many websites serve this information through a documented application programmer interface (API). These webservice APIs provide a mechanism to create new functionality on top of existing webcontent.
While there are several ways to implement webservices, Representational State Transfer (REST) has gained widespread popularity. REST is more of a style than a standard. A system designed in the REST style is called RESTful. RESTful systems typically use HTTP requests to query and post data using the standard HTTP verbs (GET, POST, PUT, DELETE, etc.). Often some form of authentication is necessary to communicate with a webservice. It is common to use OAuth for this purpose.
Data serialization¶
When you use a web browser to view a webpage, your browser handles the HTTP communication for you. You specify what you wish to view in the form of a URI such as http://example.org/absolute/URI/with/absolute/path/to/resource.txt. At this point your browser communicates with the webserver and requests the resource. The resource is typically provided to your web browser as an HTML document, which browsers are specifically designed to render.
Similarly, you will use HTTP to communicate with webservices such as Twitter. However rather than passively consuming webpages, you will be interested in retrieving data in a form that is amenable to further processing.
Data serialization refers to the process of encoding data structures and objects in a format that can be used to store this information on disk or transmit it over the web. For example, in R you can use the Rdata format to save R objects to disk and reload them later. For webservices, JSON and XML are standard formats. To better understand this, let’s briefly look at data serialization more generally.
Python object¶
First let’s create a Python object:
mydict = {
"parents": [{"name": "mom",
"number": "555-123-4567"},
{"name": "dad",
"number": "555-123-4567"}],
"colleagues": {"name": "advisor",
"number": "555-123-4567"}
}
And let’s print the results:
>>> mydict
{'colleagues': {'name': 'advisor', 'number': '555-123-4567'}, 'parents': [{'name': 'mom', 'number': '555-123-4567'}, {'name': 'dad', 'number': '555-123-4567'}]}
That is not nicely formatted, so let’s us the pretty printing module:
>>> import pprint
>>> pprint.pprint(mydict)
{'colleagues': {'name': 'advisor', 'number': '555-123-4567'},
'parents': [{'name': 'mom', 'number': '555-123-4567'},
{'name': 'dad', 'number': '555-123-4567'}]}
XML¶
How does this object look if we convert it to XML? [1]
First you will need to install dict2xml:
$ pip install dict2xml
Now you can do the following in Python:
>>> from dict2xml import dict2xml
>>> print(dict2xml(mydict))
<colleagues>
<name>advisor</name>
<number>555-123-4567</number>
</colleagues>
<parents>
<name>mom</name>
<number>555-123-4567</number>
</parents>
<parents>
<name>dad</name>
<number>555-123-4567</number>
</parents>
JSON¶
What if we convert it to JSON?
>>> import json
>>> print(json.dumps(mydict, indent=4, sort_keys=True))
{
"colleagues": {
"name": "advisor",
"number": "555-123-4567"
},
"parents": [
{
"name": "mom",
"number": "555-123-4567"
},
{
"name": "dad",
"number": "555-123-4567"
}
]
}
YAML¶
What if we convert it to YAML?
>>> import yaml
>>> print(yaml.dump(mydict))
colleagues: {name: advisor, number: 555-123-4567}
parents:
- {name: mom, number: 555-123-4567}
- {name: dad, number: 555-123-4567}
Questions¶
Looking over the output of the above formats you should notice several things.
- Which of the formats uses the largest number of characters?
- Which uses the fewest?
- Which looks most like Python?
Reading and writing JSON¶
To save mydict as a JSON file, you could do the following:
>>> outfile = open("data.json", "w")
>>> json.dump(mydict, outfile, indent=4, sort_keys=True)
>>> outfile.close()
I prefer to use a context manager which handles closing the file handle for me:
>>> with open("data.json", "w") as outfile:
... json.dump(mydict, outfile, indent=4, sort_keys=True)
To load the JSON file, you could do the following:
>>> infile = open("data.json")
>>> mydict = json.load(infile)
>>> infile.close()
Or using a context manager:
>>> with open("data.json") as infile:
... mydict = json.load(infile)
Your JSON file will have nested and non-homogeneous structure, which is not
possible to directly store using CSV. So you will need to first decide what
data you want to save as CSV and then transform the JSON data into the
necessary form. Here is an example of how you might transform mydict above
into a list of equal length tuples:
>>> mydict["colleagues"] = [mydict["colleagues"]]
>>> mylist = [(e["name"], e["number"], k)
... for k, v in mydict.items()
... for e in v]
Before I can use list comprehension to form the list of tuples I ensure that the nested structure that I iterate over has equal depth in each substructure. Then I save the list of tuples as a CSV file:
>>> import csv
>>> with open("data.csv", "w") as outfile:
... csv_out = csv.writer(outfile)
... csv_out.writerow(["name", "number", "relation"])
... for row in mylist:
... csv_out.writerow(row)
Word Vectors¶
In many statistical applications, data are represented as vectors in some space. For instance, in genomic applications measurements for gene expression levels may be recorded for several subjects. Each of these subjects is then represented as a vector in gene space where each dimension represents the expression level of a specific gene.
In other applications, the data is not directly presented as a vector space model; yet may be usefully represented as such. In this tutorial, you will see one common way to represent text documents as vectors. Once we’ve represented text documents as vectors we will want to ask which documents are similar to each other. We could use the dot product or cosine of the angle between two document vectors as our measure of similarity; however, in the second homework you will use another distance measure that has proved fruitful for measuring similarity in text documents.
Bag of words model¶
Natural languages encode part of the meaning of a text in the specific order of the words as the following two sentences illustrate:
John ate the tomato.
The tomato ate John.
For some tasks, however, it suffices to consider only the number of occurrences of each word in a document—disregarding grammar and word order. Such a simplified representation of a document is called a bag of words model.
To get a sense of why this simple model might be useful consider the task of distinguishing documents pertaining to cars from documents about flowers. In documents related to cars you might expect to see many occurrences of words like power, drive, wheel, etc. Similarly, in the documents about flowers you might expect to see many occurrences of words like petal, bud, seed, etc.
To see how we could use this insight in practice, consider the following three simple text documents (i.e., consider each sentence a separate document):
R is a popular programming language for statistical computing.
The Python programming language is also popular for statistical programming.
Spanish is a popular foreign language taught in US schools.
Based on these three documents, we can create the following list of words used in our collection of documents (let’s call this our vocabulary):
['a',
'also',
'computing',
'for',
'foreign',
'in',
'is',
'language',
'popular',
'programming',
'python',
'r',
'schools',
'spanish',
'statistical',
'taught',
'the',
'us']
For each word in the above list of 18 words, we can count how many times it occurs in the first text document to create the word vector
[1, 0, 1, 1, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 0, 0]
where each element of the word vector is the number of times the
corresponding word from our list of vocabulary words appears in the
first document. For example, the first 1 in the above word vector
represents the fact that the word a appears exactly once in the
sentence
R is a popular programming language for statistical computing.
Similarly, the first 0 represents the fact that the word also
does not occur in the sentence.
Following the same procedure for the second and third sentences in our collection of documents, yields the following two word vectors:
[1, 0, 0, 0, 1, 1, 1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0]
[0, 1, 0, 1, 0, 0, 1, 1, 1, 2, 0, 0, 0, 0, 1, 0, 0, 0]
Term-document matrix¶
Putting the list of vocabulary words used in our collection of documents as well as the word vector for each document under the bag of words model, we can form the following term document matrix:
Document 1 Document 2 Document 3
a 1 1 0
also 0 0 1
computing 1 0 0
for 1 0 1
foreign 0 1 0
in 0 1 0
is 1 1 1
language 1 1 1
popular 1 1 1
programming 1 0 2
python 0 0 0
r 0 0 0
schools 0 1 0
spanish 0 0 0
statistical 1 0 1
taught 0 1 0
the 0 0 0
us 0 0 0
where each row of the matrix corresponds to the given term from our vocabulary and each column represents one document from our collection.
One purpose of representing the collection of documents as a matrix of word vector columns is that we can measure the “distance” between any two column vectors in our term document matrix to get a sense of how similar the corresponding documents are.
The dot-product between word vectors is a simple approach to measuring the similarity of the corresponding documents. We will see better alternatives to this measure later, but for now let’s just consider this simple “distance” measure. Recall that the dot-product \(\mathbf{a} \cdot \mathbf{b}\) between two vectors \(\mathbf{a}\) and \(\mathbf{b}\) is the sum of products of the corresponding elements \(\mathbf{a} \cdot \mathbf{b} = \sum{a_i b_i}\). Taking the dot-product of all pairs of word vectors yields the following similarity matrix:
Document 1 Document 2 Document 3
Document 1 9 4 7
Document 2 4 10 3
Document 3 7 3 12
As you would expect, each document is most similar with itself. However, does it make sense to think document 3 is more similar to itself than document 2 is similar to itself? Probably not. The reason that document 3 has a higher entry in the similarity matrix based on raw word occurrence counts and the dot-product is that we aren’t controlling for the length of the document. However, notice that documents 1 and 3 are more similar (by this measure) than either documents 1 and 2 or documents 2 and 3. Since the first and third documents are both related to statistical programming languages, you would hope that our approach results in a similarity measure that results in them being closer to each other than either is to the document about natural language. Fortunately, even with this simple approach the results aren’t too far off from what you might expect.
Exercise: US Senate tweets¶
In this exercise you will explore Tweets from members of the U.S. Senate.
To get the data you can use wget (if you only have curl you can
use curl -LO instead of wget in the commands below):
$ wget http://jarrodmillman.com/rcsds/data/senators-list.json
$ wget http://jarrodmillman.com/rcsds/data/timelines.json
The first file senators-list.json is a list of US Senate Twitter accounts
[2] retrieved using the REST API [3]. The second file timelines.json
contains each Senator’s user profile [4], including their
most recent tweets (at the time I ran ran the query).
Here is the script I used to download the data:
$ wget http://jarrodmillman.com/rcsds/code/fetch_senator_tweets.py
Your task is to do the following things and answer the following questions:
- Load
senators-list.jsonassenators. - Load
timelines.jsonastimelines. - What type of datastructure is
timelines? - How many timelines are there? What does each timeline correspond to?
- Make a list of each senator’s screen name using the variable
senators. - Make a list of the number of followers each senator has.
- What is the screen name of the senator with the largest number of followers.
- Make a list called
tweetssuch that each element of the list contains all of one senator’s tweets concatenated as one string. - Create a sorted list of all the unique words used in any senators tweets and call
it
vocab.
Once you’ve constructed tweets and vocab, you will be able to run
the following code to construct term-document matrix:
import numpy as np
M = np.zeros([len(tweets), len(vocab)])
for n, tweet in enumerate(tweets):
for m, term in enumerate(vocab):
M[n, m] = tweet.count(term)
In your homework assignment you will also create a term-document matrix, but for the homework you aren’t allowed to use NumPy. Once you form a term-document matrix, there are many things you can do. Since the word vectors (i.e., columns of the term-document matrix) live in a high dimensional space, it is difficult to use our spatial intuitions to understand how things cluster. If, however, we are able to project the data into a much lower dimensional space without losing much information, then perhaps our intuitions will be helpful.
We will talk about this in more detail later, but Principle Components Analysis (PCA) is one way to reduce the dimensionality of the problem. If you want to try the following, you will need to install SciKit Learn:
$ pip install sklearn
After you’ve installed sklearn, you should be able to project the data
onto the first two principle axes as follows:
# pca using scikit-learn
from sklearn import decomposition
pca = decomposition.PCA(n_components=2)
pca.fit(M)
pc = pca.transform(M)
plt.scatter(pc[:, 0], pc[:, 1])
plt.show()
If you’ve done everything right, you should have produced something like this:
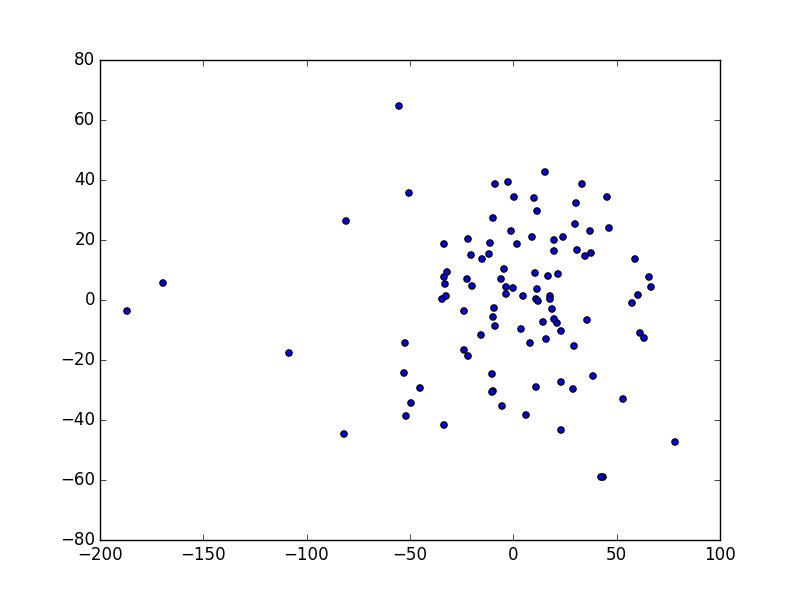
Term-document matrix projected on first and second principal axes.
Links¶
Serialization¶
- http://en.wikipedia.org/wiki/Serialization
- http://en.wikipedia.org/wiki/Comparison_of_data_serialization_formats
- http://www.json.org/xml.html
- http://yaml.org/
- http://www.drdobbs.com/web-development/after-xml-json-then-what/240151851
- http://www.cowtowncoder.com/blog/archives/2012/04/entry_473.html
| [1] | This functionality is not part of the standard library. And should not be used in practice. |
| [2] | https://twitter.com/gov/lists/us-senate/members |
| [3] | https://dev.twitter.com/rest/reference/get/lists/members |
| [4] | https://dev.twitter.com/rest/reference/get/statuses/user_timeline |
